publications
List of my publications in academic journals, reversed chronological order.
2025
2025
-
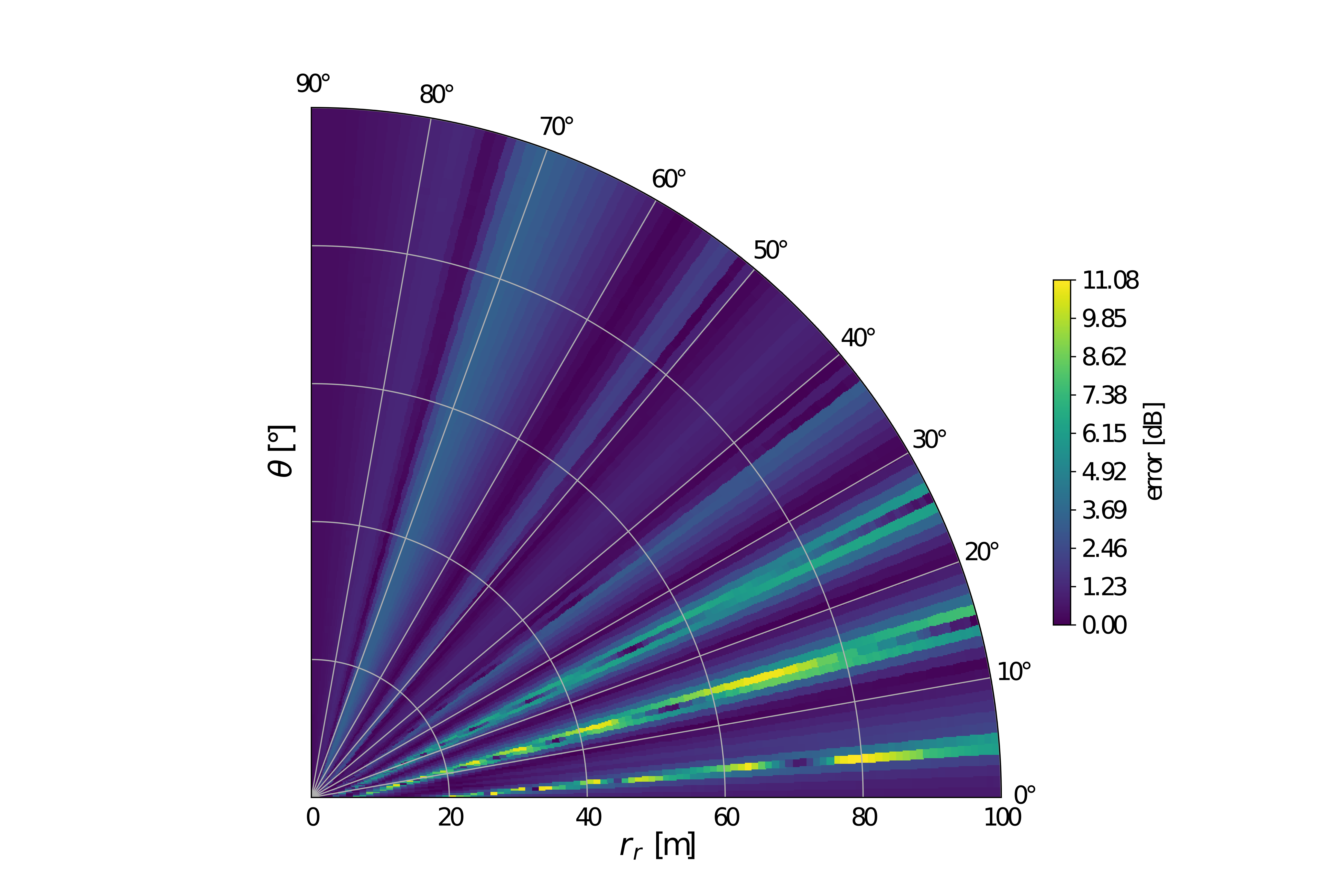 Transmission line matrix model: numerical dispersion effects on simulated specular reflectionQuentin Goestchel, Gwenaël Guillaume, David Ecotière, and 1 more authorNov 2025Publisher: EDP Sciences
Transmission line matrix model: numerical dispersion effects on simulated specular reflectionQuentin Goestchel, Gwenaël Guillaume, David Ecotière, and 1 more authorNov 2025Publisher: EDP SciencesNumerical sound propagation models include a wide range of methods with their own advantages depending on the physical phenomena under consideration. Due to its low-order scheme characteristic, the transmission line matrix (TLM) model is considered for coarse modeling of sound fields in complex outdoor environments. However, the space-time integration scheme of the method is dispersive and affects the free-field predictions. This paper extends a previous study of the numerical dispersion effect on the acoustic pressure field. An ideal case with specular reflections on a perfectly reflective ground is considered to represent the worst-case scenario, as the absence of absorption by the boundary maximizes the influence of numerical dispersion. First, a reminder of the model boundary conditions for specular reflection is provided, and the corresponding analytical solution is introduced as a reference to evaluate the reliability of the model. Then, a numerical experiment is presented and performed for different sound source characteristics. The result analysis shows that dispersion can induce misplaced interferences in the numerically simulated sound fields and the resulting errors are quantified in terms of sound pressure levels (SPL). Finally, an analytical comparison with a well-known finite difference numerical scheme gives a perspective on the TLM model performance regarding several applications.
@article{goestchel_transmission_2025, title = {Transmission line matrix model: numerical dispersion effects on simulated specular reflection}, volume = {9}, issn = {2681-4617}, url = {https://acta-acustica.edpsciences.org/articles/aacus/abs/2025/01/aacus240023/aacus240023.html}, doi = {10.1051/aacus/2025057}, pages = {72}, journaltitle = {Acta Acustica}, shortjournal = {Acta Acust.}, author = {Goestchel, Quentin and Guillaume, Gwenaël and Ecotière, David and Gauvreau, Benoit}, urldate = {2025-11-25}, year = {2025}, month = nov, langid = {english}, note = {Publisher: {EDP} Sciences}, } -
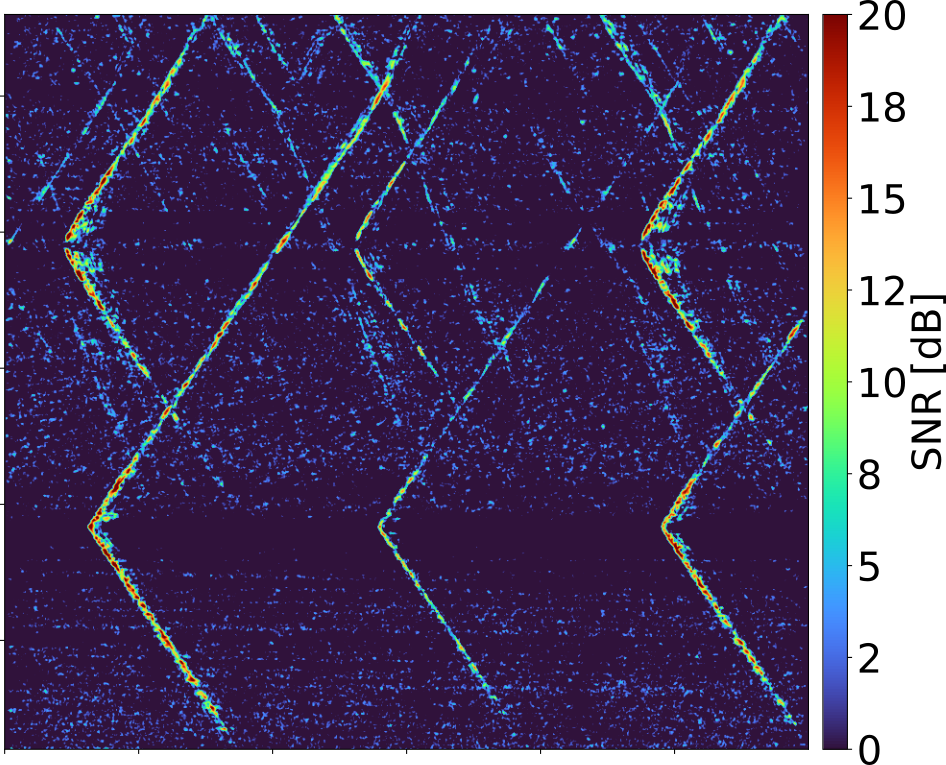 Enhancing fin whale vocalizations in distributed acoustic sensing dataQuentin Goestchel, William S. D. Wilcock, and Shima AbadiThe Journal of the Acoustical Society of America, May 2025
Enhancing fin whale vocalizations in distributed acoustic sensing dataQuentin Goestchel, William S. D. Wilcock, and Shima AbadiThe Journal of the Acoustical Society of America, May 2025Detecting and locating marine mammals is essential for understanding their behavior and supporting conservation efforts. Acoustic methods complement visual surveys and tagging, which are often limited in spatial and temporal coverage. Fin whales are particularly suited for acoustic monitoring due to their stereotypical 20 Hz vocalizations. Distributed Acoustic Sensing (DAS) offers a promising addition to hydrophone data, using fiber-optic cables as sensors for continuous, high-resolution monitoring over distances up to about 100 km. In November 2021, a DAS dataset was collected using the Ocean Observatories Initiative Regional Cabled Array, capturing valuable data on fin whale vocalizations. This dataset includes measurements from two cables with 2 m channel spacing, spanning 65 -95 km. This study evaluates various approaches—including signal-to-noise ratio estimation, matched filtering, Gabor filtering, and noise envelope subtraction—for enhancing and denoising fin whale calls in DAS data. A method that combines matched filtering and envelope subtraction is most effective at detecting even low SNR fin whale calls and obtaining arrival times. Overall, this study highlights the potential of DAS array processing to significantly improve signal-to-noise ratios and enhance detection capabilities for monitoring fin whales.
@article{goestchel_enhancing_2025, title = {Enhancing fin whale vocalizations in distributed acoustic sensing data}, volume = {157}, issn = {0001-4966}, url = {https://doi.org/10.1121/10.0036696}, doi = {10.1121/10.0036696}, number = {5}, urldate = {2025-05-14}, journal = {The Journal of the Acoustical Society of America}, author = {Goestchel, Quentin and Wilcock, William S. D. and Abadi, Shima}, month = may, year = {2025}, pages = {3655--3666}, } -
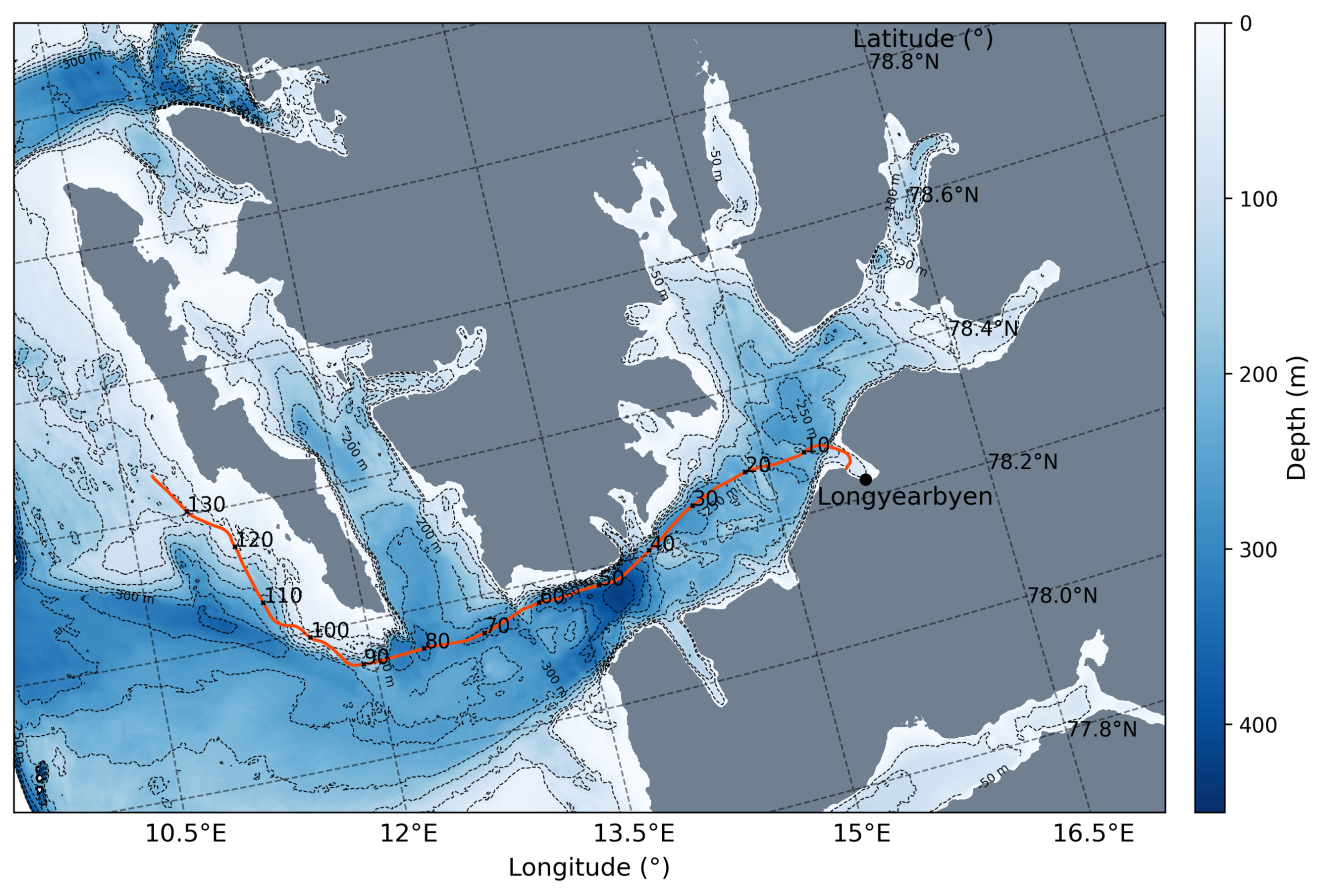 Estimating sound pressure levels from distributed acoustic sensing data using 20 Hz fin whale callsLéa Bouffaut, Quentin Goestchel, Robin André Rørstadbotnen, and 3 more authorsJASA Express Letters, Apr 2025
Estimating sound pressure levels from distributed acoustic sensing data using 20 Hz fin whale callsLéa Bouffaut, Quentin Goestchel, Robin André Rørstadbotnen, and 3 more authorsJASA Express Letters, Apr 2025Distributed acoustic sensing (DAS) is a promising technology for underwater acoustics, but its instrumental response is still being investigated to enable quantitative measurements. We use fin whale 20 Hz calls to estimate the conversion between DAS-recorded strain and acoustic pressure. Our method is tested across three deployments on varied seafloor telecommunication cables and ocean basins. Results show that after accounting for well-established DAS response factors, a unique value for water compressibility provides a good estimate for the conversion. This work represents a significant step forward in characterizing DAS for marine monitoring and highlights potential limitations related to instrument noise floor.
@article{bouffaut_estimating_2025, title = {Estimating sound pressure levels from distributed acoustic sensing data using 20 {Hz} fin whale calls}, volume = {5}, issn = {2691-1191}, url = {https://doi.org/10.1121/10.0036351}, doi = {10.1121/10.0036351}, number = {4}, urldate = {2025-04-23}, journal = {JASA Express Letters}, author = {Bouffaut, Léa and Goestchel, Quentin and Rørstadbotnen, Robin André and Sladen, Anthony and Hartog, Arthur and Klinck, Holger}, month = apr, year = {2025}, pages = {040802}, }
2023
2023
-
 Acoustic Propagation in Forest Environments. Time domain numerical methods toward bioacoustic applications.Quentin GoestchelOct 2023
Acoustic Propagation in Forest Environments. Time domain numerical methods toward bioacoustic applications.Quentin GoestchelOct 2023This manuscript investigates sound propagation modeling in forest environments, intending to understand the limitations ofexisting models and explore their potential bioacoustic applications. The subject is introduced by presenting current concernsabout the impact of noise on health and biodiversity. A literature review examines previous studies and existing outdoor soundpropagation models, both analytical and numerical, for their applicability to forest scenarios. Then, as a time-domain solver, theTransmission Line Matrix (TLM) model is thoroughly investigated, and the update of its theory allows for highlighting limitationswhen modeling outdoor long-range sound propagation. Numerical experiments are presented to quantify the subsequent errorsand limitations in the TLM model. The computational implications of modeling a significant number of points implied by largefrequency-distance ratios are discussed. Finally, some applications to model sound propagation within forests, with multipleimpedance boundary conditions, are presented, and a validation method is proposed through comparisons with in-situmeasurements at the Nouragues research station (French Guiana). Overall, this research contributes to the understanding ofhow to simulate sound propagation within forests and the potential practical applications that can arise from it.
@phdthesis{Goestchel2023c, title = {Acoustic Propagation in Forest Environments. {{Time domain numerical methods}} toward {{bioacoustic applications}}.}, author = {Goestchel, Quentin}, year = {2023}, month = oct, langid = {english}, url = {https://theses.hal.science/tel-04357383}, }
2022
2022
-
 Properties of the Transmission Line Matrix Model for Outdoor Sound Propagation: Numerical Dispersion EffectsQuentin Goestchel, Gwenael. Guillaume, David. Ecotière, and 1 more authorIn International Congress on Acoustics, Oct 2022
Properties of the Transmission Line Matrix Model for Outdoor Sound Propagation: Numerical Dispersion EffectsQuentin Goestchel, Gwenael. Guillaume, David. Ecotière, and 1 more authorIn International Congress on Acoustics, Oct 2022Time-domain numerical methods are attractive tools for the prediction of outdoor sound propagation as they are able to handle most of the physical phenomena involved in environmental acoustics. The transmission line matrix (TLM) method is considered for modelling sound fields in complex outdoor environments but it remains relatively poorly documented. In this paper, the space-time integration scheme of the method and a stability analysis are provided. The review of the model highlights similarities with a finite difference scheme and leads to a more robust understanding of its link with the wave equation using Taylor expansions. The stability analysis allows the numerical dispersion relation of the model to be formulated and the associated errors to be quantified. Two different numerical experiments are presented to characterize precisely the limitations of the method applied to outdoor sound propagation. To conclude, the results are analyzed, highlighting the effects of the propagation distance and the spectral distribution of the simulated sources.
-
 Analysis of the Numerical Properties of the Transmission Line Matrix Model for Outdoor Sound PropagationQuentin Goestchel, Gwenael. Guillaume, David. Ecotière, and 1 more authorJournal of Sound and Vibration, Aug 2022
Analysis of the Numerical Properties of the Transmission Line Matrix Model for Outdoor Sound PropagationQuentin Goestchel, Gwenael. Guillaume, David. Ecotière, and 1 more authorJournal of Sound and Vibration, Aug 2022Outdoor sound propagation modeling can be performed through various numerical models. Nowadays, time-domain methods are widely used and enable accurate simulations for most of the sound physical phenomena involved in environmental acoustics. However, the transmission line matrix (TLM) method remains relatively poorly documented. In this paper, a thorough review of the method and a stability analysis are provided. The review of the model leads to a more robust understanding of its link with the wave equation using Taylor expansions. Two different cases are considered: a homogeneous non-dissipative medium and an inhomogeneous dissipative one. The stability analysis shows the quantification of the model inherent dispersion error and highlights similarities with a finite difference scheme. To conclude, a numerical experiment aims to characterize precisely the limitations of the method applied to outdoor sound propagation.
2018
2018
-
 The P.E.T. Comfort Index: Questioning the ModelEdouard Walther and Quentin GoestchelBuilding and Environment, Jun 2018
The P.E.T. Comfort Index: Questioning the ModelEdouard Walther and Quentin GoestchelBuilding and Environment, Jun 2018[link to full text download on Elsevier https://authors.elsevier.com/a/1Wq~-1HudMvux8 (valid until May 25th 2018)] This work is a first thorough presentation of the widely used PET (Physiological Equivalent Temperature) comfort index. It underlines the simplifications made in solving the equation system for the PET and proposes a correction of the errors in the widespread version of the PET calculation routine. A comparison of the corrected model with a stringent solving of the equation system is made: as a result, the PET calculated after the original method introduces a bias of - 0.5 to + 2.3 [K] in the studied conditions (operative temperature, high mean radiant temperature and windy environments). The original vapour diffusion model is also examined and shows no dependency to the clothing level. The comparison with a state-of-the-art vapour transfer model exhibits a significant - 7 to + 2.6 [K] discrepancy with the corrected PET model in the aforementioned studied conditions. Links to the two versions of the code are provided in the appendix.